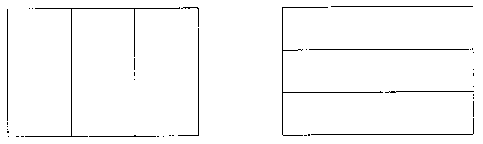
FIGURA 1. Utilización de un tablero maya.
Si a tí te preguntaran "¿Sabes sumar y multiplicar?," inmediatamente responderías: "desde luego", "claro que sí", "hasta la pregunta ofende", etc. Sin embargo, tú puedes hacer esta afirmación porque sabes que estas operaciones son de lo más sencillas, y todo gracias a que nuestro sistema decimal es muy sencillo de operar. Pero esto es debido a que, en nuestro sistema de numeración, se encuentra un número que es muy importante en cualquier sistema posicional: sí, has acertado, es el número cero. Ya que de el concepto cero se deriva el principio de posición de la numeración, y es por eso que nosotros gozamos de un sistema de numeración posicional completo.
Pues bien, ahora te retamos a que sumes y multipliques en otro sistema posicional muy completo, de una civilización tan avanzada como lo fue la civilización maya. Con ello te darás cuenta del gran adelanto que tuvo esta civilización, al ser la primera en inventar el número cero.
Los mayas (500a.C.), una de las culturas prehispánicas más brillantes de América, se adelantaron a los hindúes por lo menos en un milenio, pues usaron el cero en su sistema vigesimal posicional de numeración1 desde antes de nuestra era. Lo consideraban como el germen de los números, por lo que lo denominaremos He que significa huevo, también lo denominaron Mixbaal. Lo representaron por medio de un símbolo semejante a una concha y, de acuerdo con su religión cósmica, consideraron al cero como el caos, creador del Universo y del Sol (germen de la vida humana). Por lo tanto representaba ni la nada ni el vacío, pues según los mayas el vacío absoluto es imposible.
Para operar los numerales, los mayas se servían de un sencillo tablero, formado de columnas y renglones, donde fácilmente manipulaban con sus semillas y varitas. Debes recordar que los mayas sólo empleaban tres numerales: un punto para representar las unidades, una línea para representar el número cinco y por último al cero En cada columna del tablero representaban un número y los renglones considerados de abajo hacia arriba servían para señalar el orden de las unidades (figura 1).

FIGURA 1. Utilización de un tablero maya.
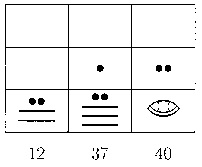
FIGURA 2. Representaciones del 12, el 37 y el 40 en un tablero maya.
Consideremos un ejemplo; en el tablero mostrado en la figura 2 tenemos:
Sumemos estos numerales como lo hacían los mayas; para sumar (buc-xicil) los mayas realizaban los siguientes pasos:
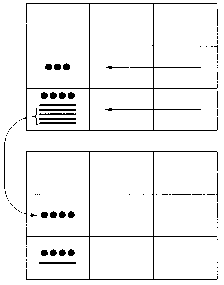
FIGURA 3. 12 +37 +40.
El resultado se interpreta muy fácilmente (figura 4):
es nuestro sistema base 10.

FIGURA 4. Interpretación del resultado de la suma 12 + 37 + 40.
Ejercicio 1. Ahora te toca a tí ponerte a prueba,2 sumando3 los siguientes numerales: 100, 1 007 y 135 (figura 5).
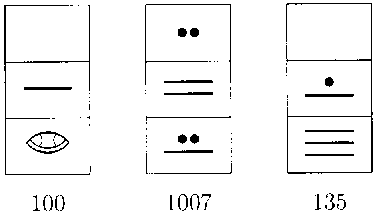
FIGURA 5. Representación maya de 100, 1007 y 35.

FIGURA 6. Representación Maya de 103 y 46.
Calcularemos el producto de 103 y 46 (figura 6) para ilustrar la forma en que los mayas multiplicaban; para multiplicar (dzaac-xoc), los mayas colocaban los factores fuera de la casillas del ingenioso tablero cuadriculado y procedían de la siguiente manera:

FIGURA 7. Colocación de los factores.

FIGURA 8. Multiplicación de por los numerales del otro factor.

FIGURA 9. Multiplicación de por los numerales del otro factor.

FIGURA 10. Sumamos los numerales en diagonal para obtener el producto.
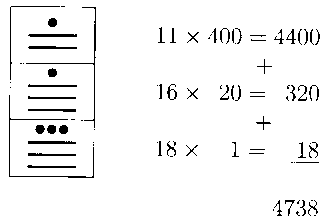
FIGURA 11. Interpretación del resultado del producto 103 × 46.
Analizando el producto (figura 11) vemos que el resultado es:
en nuestro sistema base 10.
Ejercicio 2. Ahora es tu turno: multiplica 920 por 407 (figura 12).

FIGURA 12. Representación maya de 920 y 407.
1 Para ser más precisos, el sistema de
numeración posicional maya es vigesimal, excepto por una
posición, la del tercer nivel (siga leyendo). Sus valores de
posición eran:
20 de la unidad más baja, kines (día), constituye 1
uinal;
18 uinales forman un tun (360 días, un año
aproximadamente);
20 tunes hacen un katun (7 200 días);
20 katunes hace un ciclo (144 000 días);
20 ciclos hacen un gran ciclo (2 880 000 días).
Por simplicidad, asumiremos que no había excepciones.
2 Para la siguiente revista, sabrás si tus resultados han sido correctos; en la sección "A pensar se ha dicho" aparecerán las soluciones a los ejercicios de este artículo. ¡Suerte!
3 Recuerda que hemos supuesto por simplicidad que el sistema de numeración maya era vigesimal sin accidentes, i.e., sin excepciones: hemos asumido que a partir de la segunda posición el orden de las unidades en una posición es veinte veces mayor que en la posición anterior.